| Definitions | x(s), es-causl(es; e; e'), P  Q, s = t, loc(e), es-locl(es; e; e'), Q, s = t, loc(e), es-locl(es; e; e'),  x:A. B(x), es-E(es), P x:A. B(x), es-E(es), P   Q, Q,  A, let x,y = A in B(x;y), t.1, x:A A, let x,y = A in B(x;y), t.1, x:A  B(x), guard(T), wellfounded{i:l}(A; x,y.R(x;y)), x:A B(x), guard(T), wellfounded{i:l}(A; x,y.R(x;y)), x:A  B(x), event_system{i:l}, void, isect(A; x.B(x)), top, constant_function(f; A; B), band(p; q), qpositive(r), bor(p; q), q_le(r; s), qadd_grp, grp_le(g), grp_leq(g; a; b), qle(r; s), tag(k), lnk(k), tl(l), if a<b then c else d, i <z j, i B(x), event_system{i:l}, void, isect(A; x.B(x)), top, constant_function(f; A; B), band(p; q), qpositive(r), bor(p; q), q_le(r; s), qadd_grp, grp_le(g), grp_leq(g; a; b), qle(r; s), tag(k), lnk(k), tl(l), if a<b then c else d, i <z j, i  z j, nth_tl(n;as), hd(l), l[i], rec-case(a) of [] => s | x::y => z.t(x;y;z), ||as||, (x z j, nth_tl(n;as), hd(l), l[i], rec-case(a) of [] => s | x::y => z.t(x;y;z), ||as||, (x  l), isrcv(k), -n, r * s, r - s, n + m, r + s, s+r, let x = a in b(x), when-after(e;info;pred?;init;Trans;val;time), state_when(e), outr(x), act(k), val-axiom(E;V;M;info;pred?;init;Trans;Choose;Send;val;time), Msg(M), type List, <a, b>, inl x , rcv(l,tg), inr x , locl(a), kind(e), islocal(k), kindcase(k; a.f(a); l,t.g(l;t)), Knd, n * m, isint(z;a;b), qeq(r; s), nequal(T; a; b), int_nzero, b-union(A; B), quotient(A; x,y.B(x;y)), rationals, EState(T), source(l), A l), isrcv(k), -n, r * s, r - s, n + m, r + s, s+r, let x = a in b(x), when-after(e;info;pred?;init;Trans;val;time), state_when(e), outr(x), act(k), val-axiom(E;V;M;info;pred?;init;Trans;Choose;Send;val;time), Msg(M), type List, <a, b>, inl x , rcv(l,tg), inr x , locl(a), kind(e), islocal(k), kindcase(k; a.f(a); l,t.g(l;t)), Knd, n * m, isint(z;a;b), qeq(r; s), nequal(T; a; b), int_nzero, b-union(A; B), quotient(A; x,y.B(x;y)), rationals, EState(T), source(l), A  B, B,  , SWellFounded(R(x;y)), link(e), EOrderAxioms(E;pred?;info), IdLnk, t , SWellFounded(R(x;y)), link(e), EOrderAxioms(E;pred?;info), IdLnk, t  T, Unit, left + right, T, Unit, left + right,  , EqDecider(T), es-pred?(es), axiom, , EqDecider(T), es-pred?(es), axiom,  , sender(e), rcv?(e), "$token", outl(x), pred(e), isl(x), , sender(e), rcv?(e), "$token", outl(x), pred(e), isl(x),   b, first(e), pred!(e;e'), n - m, if a=b then c else d, (i = b, first(e), pred!(e;e'), n - m, if a=b then c else d, (i =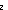 j), if b then t else f fi , Y, rel_exp(T; R; n), x f y, a < b, j), if b then t else f fi , Y, rel_exp(T; R; n), x f y, a < b,  , {x:A| B(x)} , , {x:A| B(x)} ,  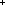 , ,  x.A(x), rel_plus(T; R), e < e', es_info(es), t.2, destination(l), case b of inl(x) => s(x) | inr(y) => t(y), ecase1(e;info;i.f(i);l,e'.g(l;e')), loc(e), atom{$n:n}, Id, prop{i:l}, x.A(x), rel_plus(T; R), e < e', es_info(es), t.2, destination(l), case b of inl(x) => s(x) | inr(y) => t(y), ecase1(e;info;i.f(i);l,e'.g(l;e')), loc(e), atom{$n:n}, Id, prop{i:l},   x. t(x), False x. t(x), False |